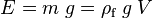En física, el principio de Pascal o ley de Pascal, es una ley enunciada por el físico y matemático francés Blaise Pascal (1623-1662) que se resume en la frase: la presión ejercida en cualquier parte de un fluido incompresible y en equilibrio dentro en un recipiente de paredes indeformables, se transmite con igual intensidad en todas las direcciones y en todos los puntos del fluido.
El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el émbolo, se observa que el agua sale por todos los agujeros con la misma velocidad y por lo tanto con la misma presión.
El principio de Pascal puede ser interpretado como una consecuencia de la ecuación fundamental de la hidrostática y del carácter altamente incompresible de los líquidos. En esta clase de fluidos la densidad es prácticamente constante, de modo que de acuerdo con la ecuación:
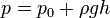
Donde:
 , presión total a la profundidad.
, presión total a la profundidad. , presión sobre la superficie libre del fluido.
, presión sobre la superficie libre del fluido. , densidad del fluido.
, densidad del fluido. , aceleración de la gravedad.
, aceleración de la gravedad. , Altura, medida en Metros.
, Altura, medida en Metros.
La presión se define como la fuerza ejercida sobre unidad de área p = F/A. De este modo obtenemos la ecuación: F1/A1 = F2/A2, entendiéndose a F1 como la fuerza en el primer pistón y A1 como el área de este último. Realizando despejes sobre este ecuación básica podemos obtener los resultados deseados en la resolución de un problema de física de este orden.
Si se aumenta la presión sobre la superficie libre, por ejemplo, la presión total en el fondo ha de aumentar en la misma medida, ya que el término ρgh no varía al no hacerlo la presión total. Si el fluido no fuera incompresible, su densidad respondería a los cambios de presión y el principio de Pascal no podría cumplirse. Por otra parte, si las paredes del recipiente no fuesen indeformables, las variaciones en la presión en el seno del líquido no podrían transmitirse siguiendo este principio.